Mô tả
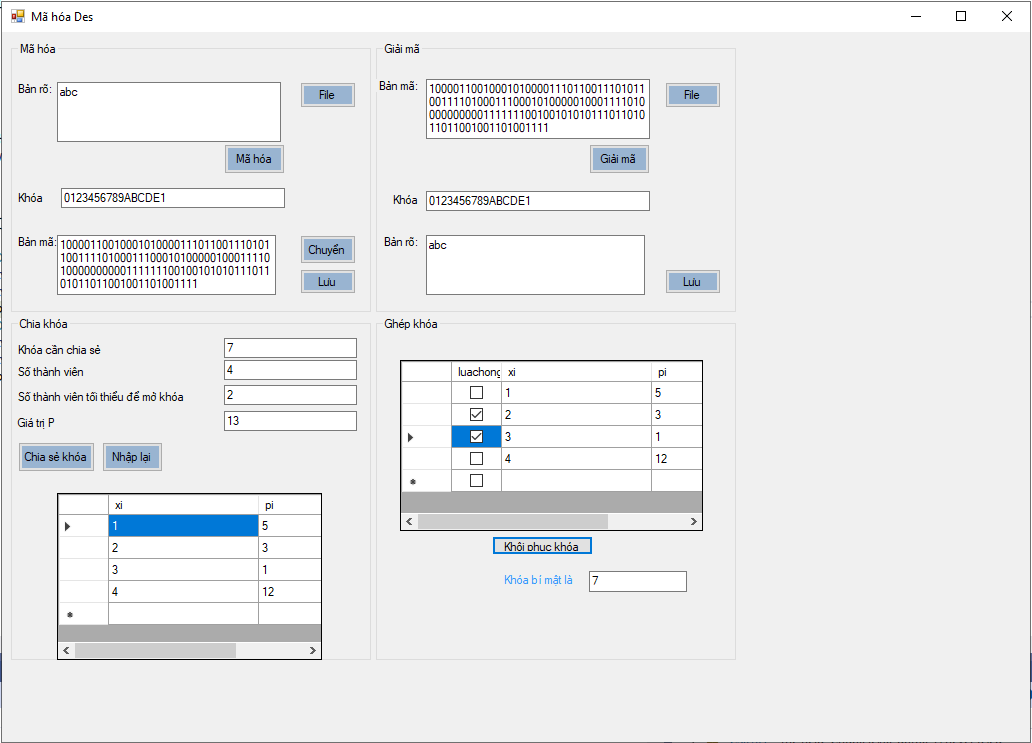
Sơ đồ chia sẻ bí mật là một phương thức để chia sẻ bí mật ra nhiều phần sau đó phân phối cho một tập hợp những người tham gia sao cho các tập con trong số những người này được chỉ thị, có khả năng khôi phục lại bí mật bằng cách kết hợp dữ liệu của họ.
Một sơ đồ chia sẻ bí mật là hoàn hảo, nếu bất kì một tập hợp những người tham gia mà không được chỉ định, sẽ không thu được thông tin về bí mật.
Cho t, w là các số nguyên dương, t ≤ w. Một sơ đồ ngưỡng A(t, w) là một phương pháp phân chia khóa K cho một tập w thành viên (kí hiệu là P) sao cho t thành viên bất kì có thể tính được K nhưng không một nhóm (t- 1) thành viên nào có thể làm được điều đó.
Giá trị k được chọn bởi một thành viên đặc biệt được gọi là người phân phối (D). D P .
D phân chia khóa k cho mỗi thành viên trong P bằng cách cho mỗi thành viên một thông tin cục bộ gọi là mảnh. Các mảnh được phân phát một cách bí mật để không thành viên nào biết được mảnh được trao cho mỗi thành viên khác. Một tập con các thành viên (B ⸦ P) sẽ kết hợp các mảnh của họ để tính khóa k (cũng có thể trao các mảnh của mình cho một người đáng tin cậy để tính khóa hộ).
Nếu |B| ≥ t thì họ có khả năng tính được k. Nếu |B| ≤ t thì không thể tính được k.
Gọi P là tập các giá trị được phân phối khóa K: P = { pi: 1≤ i≤ w} K là tập khóa: tập tất cả các khóa có thể.
Sau đây là một sơ đồ ngưỡng được gọi là sơ đồ ngưỡng Shamir.
Giai đoạn khởi tạo:
1. D chọn w phần tử khác nhau và khác 0 trong Zp và kí hiệu chúng là: xi, 1≤ i ≤ w (w ≥ p+1).
Với 1≤ i ≤ w, D cho giá trị xi cho pi. Các giá trị xi là công khai.
Phân phối mảnh:
2. Giả sử D muốn phân chia khóa k ∈ Zp. D sẽ chọn một cách bí mật (ngẫu nhiên và độc lập) t-1 phần tử Zp, ai…ai-1
3. Với 1 ≤ i ≤ w, D tính yi = a (xi), trong đó a(x) = k+
4. Với 1 ≤ i ≤ w, D sẽ trao mảnh yi cho pi
Trong sơ đồ ngưỡng Shamir xây dựng một đa thức ngẫu nhiên a(x) có bậc tối đa là t-1. Trong đa thức này hằng số là khóa k. Mỗi thành viên pi sẽ có một điểm (xi,, yi). Ta xét một tập con B gồm t thành viên tạo lại khóa k bằng 2 phương pháp:
Phép nội suy đa thức
Công thức nội suy Lagrange
Tạo lại khóa k bằng phương pháp sử dụng phép nội suy đa thức:
Giả sử các thành viên pi, muốn xác định khóa k.
Ta biết rằng:
Yu = a(x). trong đó a(x) là một đa thức bí mật được D chọn. Vì a(x) có bậc lớn
nhất là t-1 nên ta có thể viết như sau:
a(x) = a + a₁x+......ai-1x i-1
Ta có hệ các phương trình tuyến tính (trong Zp) như sau:
a0 + a1xi1 + a2x ……..+ at-1xit1t-1 = yi1
a0 + a1xi2 + a2xi2 ……..+ at-1xitt-1 = yi2
………..
a0 + a1xi1 + a2xit ………+ at-1xittt-1 = yit
Trong đó hệ số a0, a1,..... at-1 là các phần tử chưa biết của Zp, còn ao = K là khóa.
Vì y = a(X;) nên B có thể thu được t phương trình tuyến tính t ẩn (a0, a1,..... at-1), ở đây tất cả các phép tính số học đều được thực hiện trên Zp.
Nếu các phương trình này độc lập tuyến tính thì sẽ cho ta nghiệm duy nhất và thu được giá trị khóa a.
Sau đây là một thủ tục (protocol) chia sẻ bí mật dựa trên ý tưởng của Language:
Giá sử ta có n thực thể A, ,A,......A, và có một người ủy quyền B biết được toàn bộ khóa bí mật SeN.
Người được ủy quyền B thực hiện các bước sau đây:
1. B chọn 1 số nguyên tố P đủ lớn sao cho: n << Vp. Với SeZp.
2. B, tiếp theo, chọn 2n-1 số một cách ngẫu nhiên:
a1, a2,..., an-1
vo, v1,…, vn-1
trong đó: vi≠0,vi≠vj,i≠j
3. B xác định một đa thức với các hệ số a1, a2,...., an-1 trên Zp:
f(x)= an-1xn-1+ an-2xn-2+........+a1x + s (mob P)
4. Bây giờ B gửi cho Aj một cách công khai cặp (vj ,f(vj)) với j = 0,1,2,....n-1 coi như là một mảnh riêng của Aj
Khôi phục bí mật S:
Tất cả n người A1 ,A2,......,An có thể hợp tác lại để khôi phục lại bí mật S bằng cách tính:
g(x) = Σojn f(vj) Пoin (vj-vi)-1(x-vi) mob p.
Khi đó dễ dàng xác định được S = g(0)
Ta có định lí sau: n thực thể kết hợp với nhau thì có thể khôi phục bí mật S một cách có hiệu quả đó là: S= g(0) = f(0)
Bài toán chia sẻ bí mật Lagrange
Còn được gọi là phương pháp Lagrange để chia sẻ bí mật, là một phương pháp mã hóa dữ liệu để chia sẻ một bí mật cho một nhóm người dùng mà chỉ có khi nhóm đủ đại diện mới có thể khôi phục lại bí mật ban đầu. Phương pháp này được đặt tên theo tên của nhà toán học Joseph-Louis Lagrange. Ý tưởng cơ bản của phương pháp Lagrange là chia bí mật thành các phần nhỏ hơn gọi là "phần tử bí mật" và sau đó phân phối các phần tử bí mật này cho các thành viên của nhóm. Để khôi phục lại bí mật ban đầu, cần phải có đủ số lượng thành viên trong nhóm đồng thuận hợp tác và kết hợp các phần tử bí mật mà họ sở hữu.Cách thức thực hiện bài toán chia sẻ bí mật Lagrange như sau:
Bước 1: Chọn số lượng người trong nhóm (n) và số lượng người cần đồng thuận để khôi phục bí mật (k). Thông thường, k được chọn nhỏ hơn hoặc bằng n.
Bước 2: Tạo một đa thức bậc k-1 với hệ số tự do bằng bí mật cần chia sẻ. Ví dụ, nếu bí mật là một số nguyên, có thể chọn một đa thức bậc k-1 với hệ số tự do là số nguyên đó.
Bước 3: Tính toán giá trị của đa thức tại các điểm số nguyên từ 1 đến n. Mỗi người trong nhóm sẽ nhận được một cặp giá trị (x, y), trong đó x là một số nguyên và y là giá trị tương ứng của đa thức tại x.
Bước 4: Để khôi phục lại bí mật, cần phải có ít nhất k người trong nhóm hợp tác lại. Khi đó, họ có thể sử dụng phương pháp nội suy Lagrange để tính toán giá trị bí mật ban đầu.
Phương pháp Lagrange chia sẻ bí mật đảm bảo tính bảo mật và an toàn bằng cách yêu cầu sự hợp tác của một nhóm người. Ngay cả khi một số người trong nhóm không cung cấp thông tin của mình, bí mật vẫn không thể khôi phục được. Đây là một phương pháp mã hóa được sử dụng rộng rãi trong lĩnh vực mật mã và bảo mật thông tin.




![[PTITHCM] Share code Đồ án Đề tài Quản lý vật tư CTDLGT (Thầy Thư) [PTITHCM] Share code Đồ án Đề tài Quản lý vật tư CTDLGT (Thầy Thư)](https://giaodichcode.com/storage/images/codes/22/main-1733304795.jpg)