Source code mã hóa và giải mã RSA bằng python

Mô tả

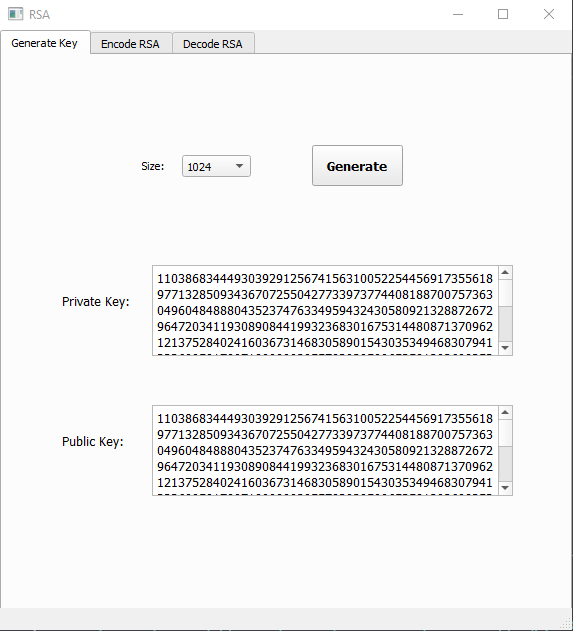
Tạo khóa

Người dùng tạo cặp khóa công khai/cá nhân:
Chọn 2 số nguyên tố lớn ngẫu nhiên p ≠ q (>120 chữ số thập phân) Tính số N = p × q, số φ(N) = (p – 1) × (q – 1)
Chọn số e ngẫu nhiên 0 < e < φ(N) sao cho: (e, φ(N)) = 1 Tính số d = e-1 mod φ(N) với 0 < d < φ(N)
Để tính số nghịch đảo d ta có thể sử dụng thuật toán Euclid mở rộng
Khóa công khai là cặp: ku = {e,N} Khóa cá nhân là cặp: kr = {d,N}
Các giá trị d, p, q và φ(N) cần được giữ bí mật
Trong khi đó các giá trị e, N được công bố công khai.
Số e thường nhỏ, có thể dùng chung một giá trị e cho nhiều người. Trước kia người ta thường hay chọn e = 3, bây giờ người ta hay chọn e = 65535. Tuy nhiên, số d tính được thì thường là rất lớn.

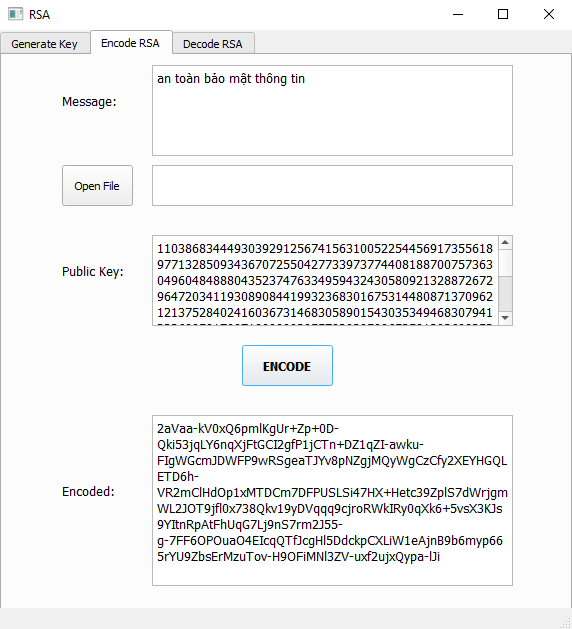
Mã hóa
Sử dụng khoá công khai đã tạo ra ở trên để mã hoá thông điệp.
Thông điệp cần mã hoá: M ( 0 < M < N );
Người gửi sử dụng khóa công khai của người nhận ku = {e, N} để mã hoá M;
Tính: C = Me mod N, với 0 < C < N.
Để tính giá trị C ta có thể sử dụng thuật toán bình phương và nhân
C chính là bản mã sẽ được gửi đi cho người nhận

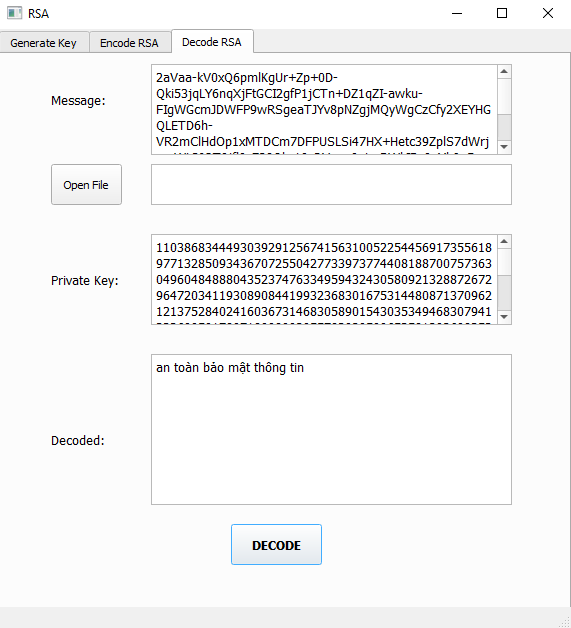
Giải mã
Sử dụng khoá cá nhân để giải mã thông điệp.
Thông điệp cần giải mã là C
Người nhận sử dụng khóa cá nhân của mình kr = {d, N} để giải mã C
Tính: M‟ = Cd mod N, với 0 < M‟ < N
Để tính giá trị M’ ta cũng có thể sử dụng thuật toán bình phương và nhân. Nếu quá trình giải mã thành công thì M’chính là bản nguồn M. Thật vậy:
Theo quá trình tạo khoá của thuật toán RSA thì các số d và e là nghịch đảo của nhau theo mod φ(N), tức là: d = e-1 mod φ(N), khi đó tồn tại số nguyên s sao cho: e × d = 1 + s × φ(N), do đó từ điều kiện mã hoá C = Me ta suy ra Cd = (Me)d = Me×d = M1+s×φ(N) = M × (Mφ(N))s ?= M × (1)s mod N = M.
Nếu ta chứng minh được Mφ(N) = 1 mod N thì chuỗi đẳng thức trên sẽ đúng và ta sẽ có điều phải chứng minh. Xét hai trường hợp có thể xảy ra:
Nếu (M, N) = 1 thì theo định lý Euler ta có: Mφ(N) = 1 mod N (đpcm).
Nếu (M, N) ≠ 1 thì vì N = p × q và p, q là hai số nguyên tố và 0 < M < N nên (M, N) = p hoặc (M, N) = q.
Không mất tính tổng quát giả sử (M, N)= p ? p|M ? M = t × p (với t là số nguyên nào đó) và khi đó: (q, M)=1 ? Mφ(q) = mod q (theo định lý Euler) ? Mφ(q) = 1 + c × q với c là số nguyên ? M × Mφ(q) = M × (1 + c × q) = M + t × p × c × q = M + t × c × N = M mod N
? Mφ(q) = 1 mod N.
Từ đây ta có: Mφ(N) = M(q-1)(p-1) = Mφ(q)×(p-1) = 1(p-1) mod N = 1 mod N (đpcm).