Mô tả
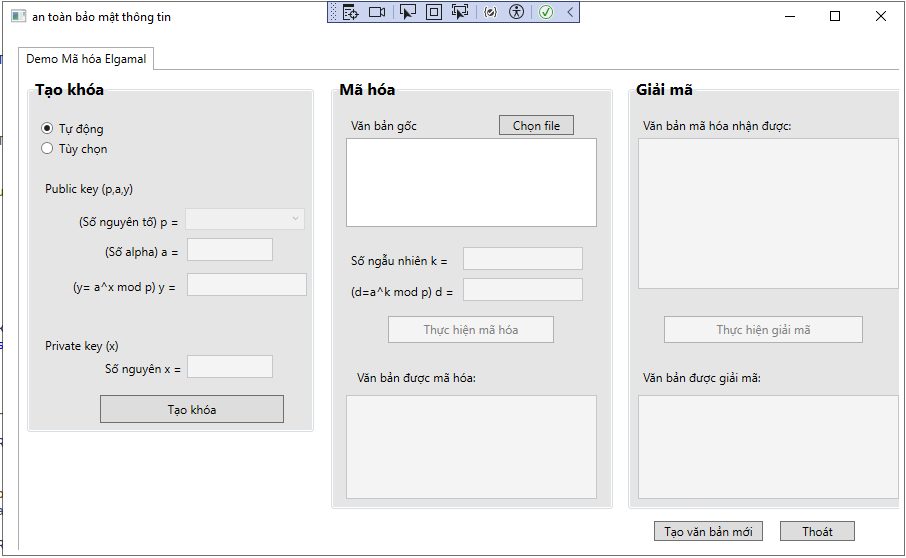
Bước 1: Tạo khóa
- Cho p là một số nguyên tố sao cho bài toán logarit rời rạc trong Zp là khó giải.
- Chọn phần tử nguyên thủy α ∈ Zp*.
- Chọn a ∈ {2, 3…, p-2} là khóa bí mật thứ nhất (Khóa người nhận, giải mã)
- Tính β = αa mod p.
- Khi đó: Kpub = (p, α, β) gọi là khóa công khai, và Kpri = (a) là khóa bí mật.
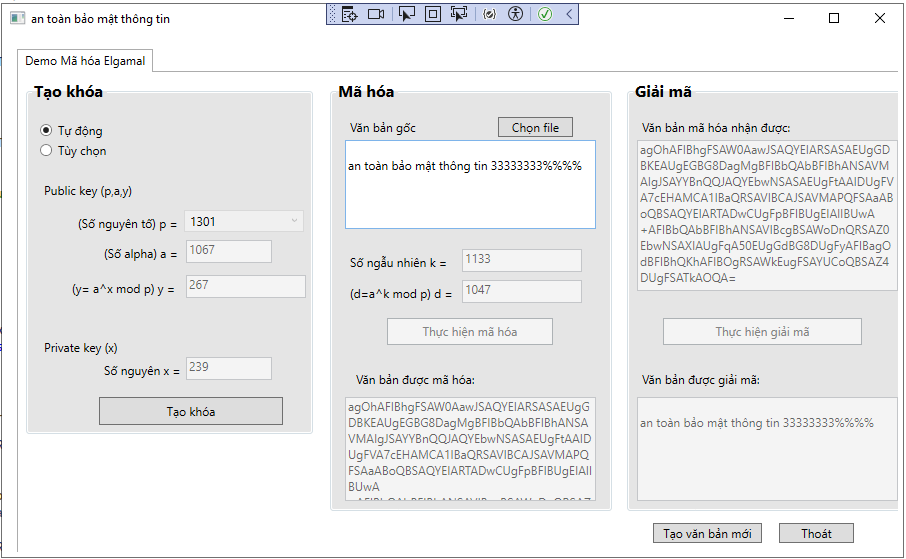
Bước 2: Xây dựng hàm mã hóa dữ liệu
- Chọn 1 số ngẫu nhiên bí mật k ∈ Zp-1, Ta xác định: k ∈ Zp-1 = {0, 1…, p-2}.
- Định nghĩa: 𝑒𝐾𝑝(𝑥, 𝑘) = (𝑦1, 𝑦2) với 𝑦1 = 𝛼𝑘𝑚𝑜𝑑𝑝 và 𝑦2 = 𝑥𝛽𝑘𝑚𝑜𝑑𝑝.
Bước 3: Giải mã
- Với y1, y2∈ Zp* ta xác định: 𝑑𝐾𝑝(𝑦1 , 𝑦2) = 𝑦2(𝑦1𝑎 ) −1𝑚𝑜𝑑 p.
A (gửi) | B (nhận) |
Choose private key KpriA=αA Compute KpubA=αaA mod p = bA bB<==B kAB = bBaA = αaA*aB mod p y = x*kAB mod p | Choose private key KpriB=αB KpubB= αaB mod p = bB A==> bA kAB = bAaB = αaB*aA mod p A==>y x = y*kAB-1 mod p |
Hướng dẫn cài đặt
- Các bạn cài đặt visual studio trước nhé.
- Dùng visual studio mở tệp vừa tải về.
- Nhấn Run là chạy được rồi 😎
- Các bước thao tác trên phần mềm các bạn xem video hướng dẫn chạy nhé.
- Chúc bạn thành công 👍✨
Hình ảnh demo
Top tìm kiếm cùng chủ đề
Code mới nhất
Bài biết mới nhất
- Top Câu Hỏi Phỏng Vấn C# Thường Gặp: Bí Quyết Thành Công
- Tổng hợp các câu hỏi phỏng vấn Java phổ biến thường gặp
- Tổng hợp các câu hỏi phỏng vấn ReactJS từ cơ bản đến nâng cao
- Load Balancer là gì? Giải Pháp Tối Ưu Cân Bằng Tải năng suất hoạt động Cho Server
- Tổng hợp các câu hỏi phỏng vấn PHP phổ biến thường gặp khi đi xin việc
- Hướng dẫn tối ưu tần số quét màn hình khi sử dụng nhiều màn hình
- 17 Công cụ tạo tiêu đề, nội dung miễn phí - Content sáng tạo chưa bao giờ đơn giản đến thế!
- Cách chơi đội hình Đấu Sĩ DTCL Mùa 11 Siêu Mạnh dễ vào Top
- Đội Hình Thần Tài trong Đấu Trường Chân Lý Mùa 11 và Cơ Chế "Nổ Hũ"
- Đội hình Pháp Sư DTCL mùa 11 mạnh nhất TFT
- Những trang website sẽ giúp bạn tìm hiểu mọi thứ trong LMHT và ĐTCL
- Đội hình Song Đấu DTCL mùa 11 mạnh nhất đấu trường chân lý
