Mô tả
Nội dung thuật toán
Thuật toán Ơ clit mở rộng tìm phần tử nghịch đảo
Cho 2 số nguyên r0, r1 tìm r1-1 theo mod r0
Intput : r0, r1
Output : r1-1 theo mod r0 (Nếu tồn tại)
● Dùng thuật toán Euclide mở rộng để tìm các số nguyên s và t sao cho s. r0 +t. r1 = gcd(r0, r1) =d
● Nếu d>1 thì r1-1 mod r0 không tồn tại. Ngược lại nếu d=1 thì return(t)
Để tìm được s, t ta dùng công thức sau :
s0 =1, t0 =0
s0 =0, t0 =1
si = s(i-2) – q(i-1)* s(i-1)
ti = t(i-2) – q(i-1)* t(i-1)
Trong đó: Với i=0,1,2,3,..
ri =qi+1*ri+1 + ri+2
Thuật toán dừng lại khi phần dư ri+2 =0
Thuật toán : Bình phương và nhân
Công thức đệ quy: để tính luỹ thừa tự nhiên bậc n của x thực hiện như sau:
Với n=0 thì xn =1
Với n>0 ta có công thức bình phương và nhân :
Như vậy phép tính xn được đệ quy về một số phép bình phương và phép nhân
Thuật toán: Sơ đồ chữ ký điện tử Elgamal
Sơ đồ chữ ký Elgamal là được viện tiêu chuẩn và vông nghệ quốc gia Mỹ sửa đổi thành chuẩn chữ ký số. Sơ đồ chữ ký Elgamal không nhất thiết phải giống như hệ thống mã hóa công khai Elgamal. Điều này có nghĩa là có nhiều chữ ký hợp lệ cho cùng một thông điệp bất kỳ . Thuật toán xác minh phải có khả năng chấp nhận bất kỳ chữ ký hợp lệ nào khi xác minh.
Sơ đồ Elgamal được định nghĩa như sau:
⮚ Tạo cặp khoá( bí mật, công khai) (a, k) :
+ Chọn phần tử nguyên tử α ϵ Zp*. Đặt P = Zp* , A = Zp* x Zp-1
+ Chọn khoá bí mật là α ϵ Zp*. Tính khoá công khai β ≡ αa mod p.
+ Định nghĩa tập khoá: ={(p, α, a, β) : β ≡ αa mod p}.
+ Các giá trị p, α, β được công khai, phải giữ bí mật a.
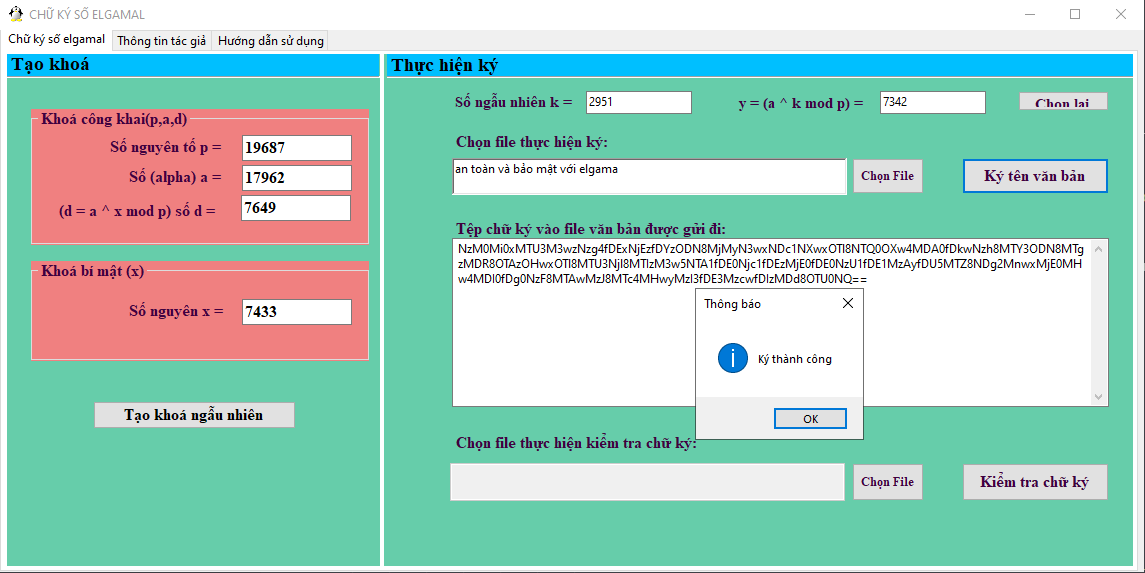
⮚ Ký số
+ Dùng 2 khoá ký: khoá a và số ngẫu nhiên k ϵ Zp-1*
+ Vì k ϵ Zp-1*, nên nguyên tố cùng p-1, do đó tồn tại k-1 mod (p-1)
+ Chữ ký trên x ϵ P là y = sigk(x, k) = (γ, δ), y ϵ A
Trong đó γ ϵ Zp*, δ ϵ Zp-1*:
γ = αk mod p và
δ= (x-a* γ) *k-1 mod (p-1)
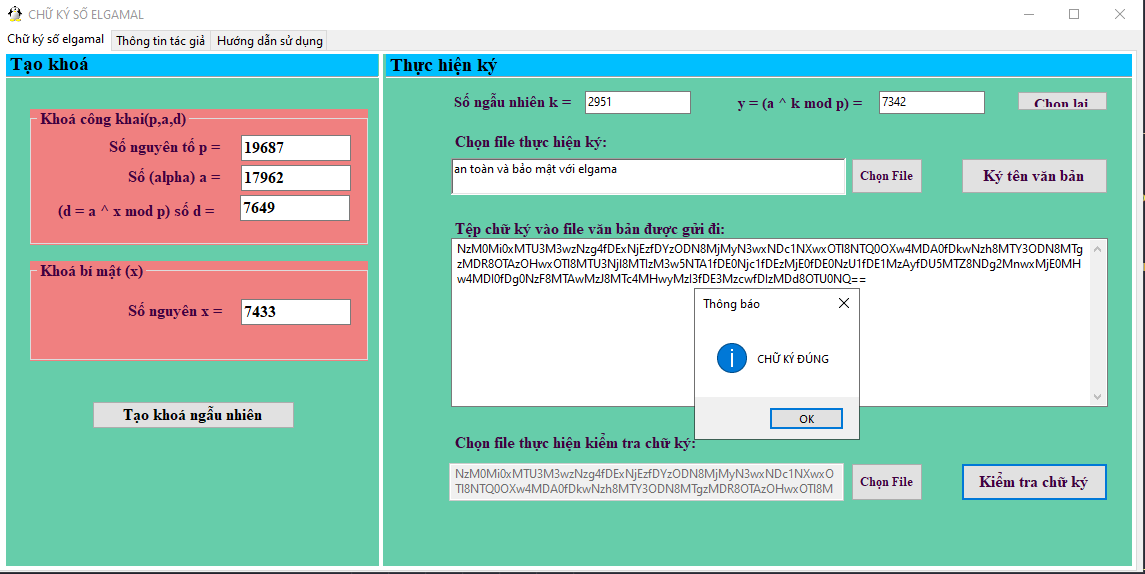
⮚ Kiểm tra chữ ký
verk (x, γ, δ)= TRUE ⬄ βγ * γδ ≡ αx mod p