Mô tả
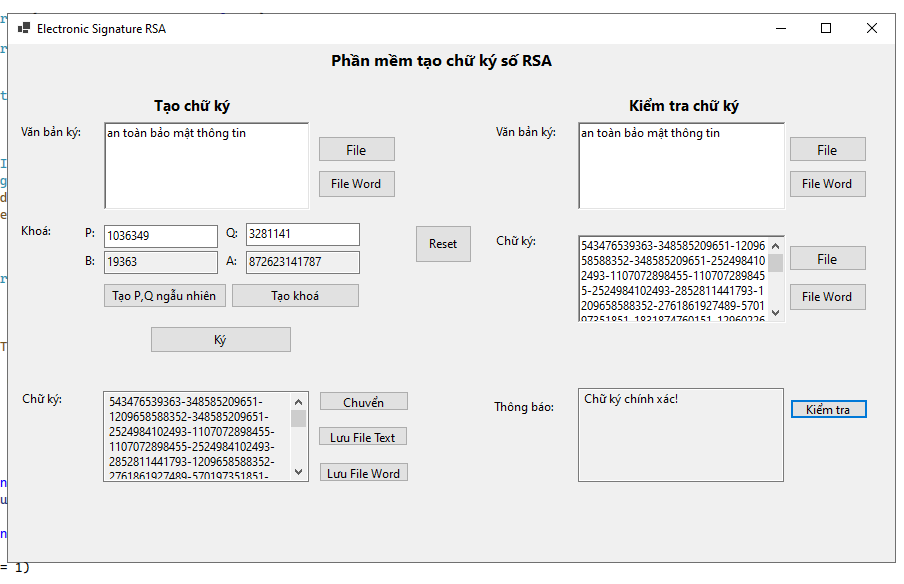
Chữ ký số là một dạng chữ ký điện tử được tạo ra bằng sự biến đổi một thông điệp dữ liệu sử dụng hệ thống mật mã không đối xứng, theo đó, người có được thông điệp dữ liệu ban đầu và khóa công khai của người ký có thể xác định được chính xác.
Khóa bí mật (Private Key): dùng để tạo ra chữ ký số RSA.
Khóa công khai (Public Key): dùng để thẩm định, kiểm tra chữ ký số và xác thực về người dùng. Khóa công khai được tạo bởi khóa bí mật tương ứng trong mỗi cặp khóa được mã hóa không đối xứng.
Người ký: đối tượng dùng khóa bí mật để ký số vào một dữ liệu nào đó thể hiện tên của mình.
Người nhận: đây là đối tượng sẽ nhận được thông điệp dữ liệu được ký số. Việc này được thực hiện thông qua việc sử dụng các chứng thư số để kiểm tra chữ ký số cho dữ liệu nhận được.
Ký số: có nhiệm vụ đưa khóa bí mật của hệ mã hóa RSA vào phần mềm tự động tạo và gắn chữ ký số cho thông điệp dữ liệu nào đó.
Sinh khóa cho hệ mã hóa RSA
Mấu chốt cơ bản của việc sinh khóa cho hệ mã hóa RSA là tìm được bộ 3 số tự nhiên e, d, n là số tự nhiên sao cho: m^(ed) ≡ m mod n
Trong đó phải đảm bảo vấn đề bảo mật cho d để dù biết e, n hay m thì cũng không thể tìm ra d.
Cụ thể, hệ mã hóa RSA được sinh khóa như sau:
- Chọn ra 2 số nguyên tố p và q.
- Tính n = pq. Lúc này n sẽ được dùng làm modulus cho khóa công khai và khóa bí mật.
- Tính một số giả nguyên tố bằng phi hàm Carmichael như sau: (n) = BCNN(λ(p), λ(q)) = BCNN(p − 1, q − 1) và cần đảm bảo giữ bí mật cho giá trị này.
- Chọn một số tự nhiên e nằm trong khoảng (1, λ(n)) sao cho e thỏa mãn điều kiện ƯCLN(e, λ(n)) = 1, tức e và λ(n) nguyên tố cùng nhau.
- Tính toán số d sao cho đảm bảo điều kiện là d ≡ 1/e (mod λ(n)) hay de ≡ 1 (mod λ(n)). Khi đó, số d được gọi là nghịch đảo modulo của e (theo modulo mod λ(n)).
- Khóa bí mật sẽ là bộ số (n, d) và khóa công khai sẽ là bộ số (n, e). Cần giữ khóa bí mật cẩn thận cũng như các số nguyên tố p và q vì từ đó mà việc tính toán các khóa sẽ trở nên dễ dàng hơn.
Thực tế, số e được chọn tương đối nhỏ để việc mã hóa và giải mã trở nên dễ dàng và nhanh chóng hơn. Giá trị e được dùng phổ biến nhất là e = 65537.
Bên cạnh đó, có thể sử dụng phi hàm Euler φ(n) = (p − 1)(q − 1) và coi nó như λ(n) để tính số giả nguyên tố. Bởi φ(n) là bội của λ(n) nên d cần thỏa mãn điều kiện de ≡ 1 (mod φ(n)) c và d ≡ 1/e (mod λ(n)).
Mã hóa khóa công khai và giải khóa khóa bí mật cho hệ mã hóa RSA
- Sau khi sinh khóa cho hệ mã hóa RSA, bước tiếp theo là mã hóa với khóa công khai (n, e) và giải mã với khóa bí mật (n, d).
- Nếu có bản rõ M thì cần chuyển nó về số tự nhiên m trong khoảng (0, n) với điều kiện m, n cùng là nguyên tố. Việc này được thực hiện bằng cách thêm kỹ thuật padding. Tiếp đến là thực hiện mã hóa m thành c theo công thức: c ≡ m^e mod n c
- Sau đó giá trị c sẽ chuyển cho người nhận và c được giải mã để lấy m theo công thức: c^d ≡ m^(de) ≡ m mod n
- Đây chính là cách đảo ngược padding để lấy m và có lại dữ liệu mã hóa.
Dưới đây là ví dụ để bạn hiểu rõ hơn về cách mã hóa với khóa công khai và giải mã với khóa bí mật:
Cho p = 5, q = 7
=> n = pq = 35
=> φ(n) = 24
Chọn e = 5 vì ƯCLN(5, 24) = 1 và chọn d = 29 vì ed – 1 = 29×5 – 1 chia hết cho 24.
Giả sử m = 32, chúng ta sẽ mã hóa m và có kết quả:
c = 32 ^ 5 % 35 = 2
Tiếp đến tiến hành thu m bằng cách giải mã c theo công thức:
m = 2 ^ 29 % 35 = 32 (đây là giá trị của m ban đầu)
Bạn có thể thử với các giá trị khác nhau của m để kiểm tra xem thuật toán có hoàn toàn chính xác hay không.
Mức độ bảo mật của hệ mã hóa RSA phụ thuộc rất nhiều vào khả năng phân tích thừa số nguyên tố của các số lớn. Lí do là vì khóa công khai được cung cấp một cách rộng rãi, việc phân tích thừa số nguyên tố đơn giản dễ dẫn đến trường hợp lộ khóa bí mật.