Mô tả
Mục đích: RSA là một thuật toán mật mã hóa khóa công khai. Đây là thuật toán đầu tiên phù hợp với việc tạo ra chữ ký điện tử đồng thời với việc mã hóa. Nó đánh dấu một sự tiến bộ vượt bậc của lĩnh vực mật mã học trong việc sử dụng khóa công cộng. RSA đang được sử dụng phổ biến trong thương mại điện tử và được cho là đảm bảo an toàn với điều kiện độ dài khóa đủ lớn.
-Mô tả sơ lược:
● Thuật toán RSA có hai khóa: khóa công khai (hay khóa công cộng) và khóa bí mật (hay khóa cá nhân). Mỗi khóa là những số cố định sử
dụng trong quá trình mã hóa và giải mã. Khóa công khai được công bố rộng rãi cho mọi người và được dùng để mã hóa. Những thông tin
được mã hóa bằng khóa công khai chỉ có thể được giải mã bằng khóa bí mật tương ứng. Nói cách khác, mọi người đều có thể mã hóa nhưng chỉ có người biết khóa cá nhân (bí mật) mới có thể giải mã được.
● Ta có thể mô phỏng trực quan một hệ mật mã khoá công khai như sau: Bình muốn gửi cho An một thông tin mật mà Bình muốn duy nhất An có thể đọc được. Để làm được điều này, An gửi cho Bình một chiếc hộp có khóa đã mở sẵn và giữ lại chìa khóa. Bình nhận chiếc hộp, cho vào đó một tờ giấy viết thư bình thường và khóa lại (như loại khoá thông thường chỉ cần sập chốt lại, sau khi sập chốt khóa ngay cả Bình cũng không thể mở lại được-không đọc lại hay sửa thông tin trong thư được nữa). Sau đó Bình gửi chiếc hộp lại cho An. An mở hộp với chìa khóa của mình và đọc thông tin trong thư. Trong ví dụ này, chiếc hộp với khóa mở đóng vai trò khóa công khai, chiếc chìa khóa chính là khóa bí mật.
-Ý tưởng và ví dụ:
● Ý tưởng về một hệ mật khoá công khai đã được Diffie và Hellman đưa ra vào 1976. Còn việc hiện thực hóa hệ mật khoá công khai thì do Rivest, Shamir và Adleman đưa ra đầu tiên vào 1977, họ đã tạo nên hệ mật RSA nổi tiếng.
● Hệ mật này sử dụng các tính toán trong Zn, trong đó n là tích của 2 số nguyên tố phân biệt p và q. Ta có thể mô tả hệ mật RSA như sau:
Cho n = p.q trong đó p và q là các số nguyên tố. Đặt P=C=Zn và định nghĩa:
K=(n,p,q,a,b):n=pq, p, q là các số nguyên tố, ab 1(mod (n))
Với K =(n,p,q,a,b) ta xác định
ek(x)=xb mod n
dk(y)=ya mod n (x,y Zn) các giá trị n và b được công khai và các giá trị p, q, a được giữ kín,
(n)=(p-1)(q-1)
Quá trình thực hiện hệ mật RSA: (người gửi: Alice; người nhận: Bob) :
● Bob tạo hai số nguyên tố lớn p và q
● Bob tính n = pq và (n) = (p-1)(q-1)
● Bob chọn một số ngẫu nhiên b (0<b< (n)) sao
cho UCLN(b, (n))=1
● Bob tính a = b-1 mod (n) bằng cách dùng thuật toán Euclide
● Bob công bố n và b trong một danh bạ và dùng chúng làm khoá công khai.
Ví dụ: giả sử Bob chọn p=101 và q=113
Khi đó n = 11413 và (n) = 100x112=11200. Vì 11200 = 26527, nên
có thể dùng một số nguyên b như một số mũ mã hoá khi và chỉ khi b không chia hết cho 2, 5 hoặc 7. Vì thế trong thực tế Bob sẽ không phân tích (n), anh ta sẽ kiểm tra điều kiện UCLN( (n),b) = 1 bằng thuật toán Euclide. Giả sử Bob chọn b = 3533, khi đó theo thuật toán Euclide mở rộng: b-1=6597 mod 11200. Bởi vậy, số mũ mật để giải mã cho Bob là a=6597. Bob sẽ công bố n = 11413 và b = 3533 trong một danh bạ. Bây giờ, giả sử Alice muốn gửi bản rõ 9726 tới Bob.
Cô ta sẽ tính 97263533 mod 11413 = 5761 rồi gửi bản mã 5761 trên kênh. Khi Bob nhận được bản mã 5761, anh ta sử dụng số mũ a mật để tính: 57616597 mod 11414 = 9726.
Với hệ mật RSA được trình bày ở trên ta thấy cách tấn công dễ thấy nhất đối với hệ mật này là thám mã cố gắng phân tích n ra các thừa số nguyên tố. Nếu thực hiện được phép phân tích này thì có thể dễ dàng tính được (n) = (p-1)(q-1) và rồi tính số mũ a và b đúng như Bob đã làm.Vì thế để hệ RSA được coi là mật thì nhất thiết n = pq phải là một số đủ lớn để việc phân tích nó sẽ không có khả năng về mặt tính toán.
-Mô tả cách hoạt động của RSA:
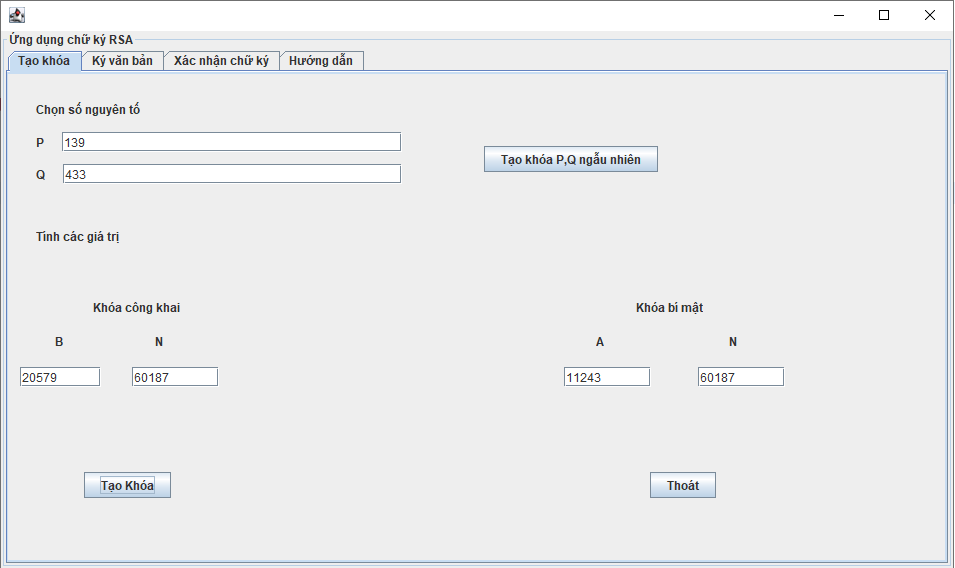
● Tạo khóa:
Giả sử An và Bình cần trao đổi thông tin bí mật thông qua một kênh không an toàn (ví dụ như Internet). Với thuật toán RSA, An đầu tiên cần tạo ra cho mình cặp khóa gồm khóa công khai và khóa bí mật theo các bước sau:
1. Chọn 2 số nguyên tố lớn p và q với p khác q , lựa chọn ngẫu nhiên và độc lập.
2. Tính: n=pq.
3. Tính: giá trị hàm số Euler (n) =(p-1)(q-1).
4. Chọn một số tự nhiên e sao cho 1<e< (n) và là số nguyên tố cùng nhau với (n).
5. Tính: d sao cho de đồng dư 1(mod (n)). Một số lưu ý:
• Các số nguyên tố thường được chọn bằng phương pháp thử xác suất.
• Các bước 4 và 5 có thể được thực hiện bằng giải thuật Euclid mở rộng.
• Bước 5 có thể viết cách khác: Tìm số tự nhiên sao cho d=(x(p-1)(q-1)+1)/e cũng là số tự nhiên. Khi đó sử dụng giá trị d mod(p - 1)(q - 1) .
● Khóa công khai:
• n, môđun, và
• e, số mũ công khai (cũng gọi là số mũ mã hóa).
● Khóa bí mật
• n, môđun, xuất hiện cả trong khóa công khai và khóa bí mật, và
• d, số mũ bí mật (cũng gọi là số mũ giải mã).
● Một dạng khác của khóa bí mật bao gồm:
• p và q, hai số nguyên tố chọn ban đầu,
• d mod (p-1) và d mod (q-1) (thường được gọi là dmp1 và dmq1),
• (1/q) mod p (thường được gọi là iqmp)
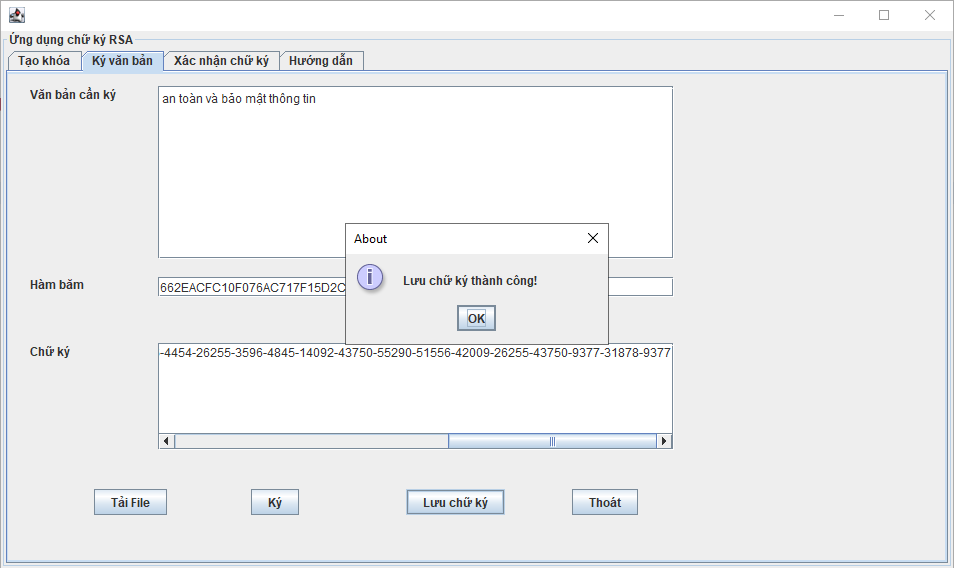
● Mã hóa:
● Giả sử Bình muốn gửi đoạn thông tin M cho An. Đầu tiên Bình chuyển M thành một số m < n theo một hàm có thể đảo ngược (từ m có thể xác định lại M) được thỏa thuận trước.
• Lúc này Bình có m và biết n cũng như e do An gửi. Bình sẽ tính c là bản mã hóa của m theo công thức.
• Hàm trên có thể tính dễ dàng sử dụng phương pháp tính hàm mũ (theo môđun) bằng (thuật toán bình phương và nhân) Cuối cùng Bình gửi cho An.
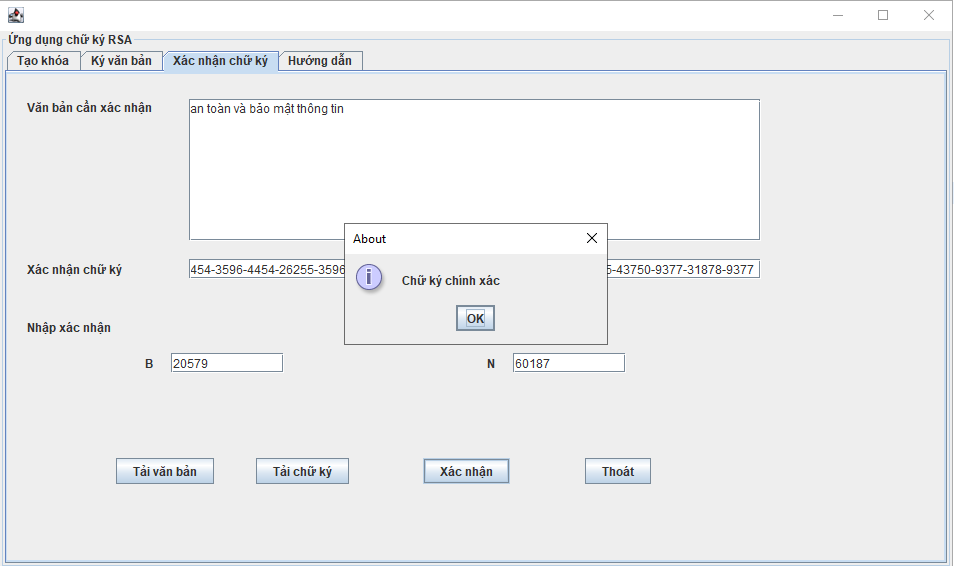
● Giải mã:
● An nhận c từ Bình và biết khóa bí mật d. An có thể tìm được m từ c theo công thức sau: m= cd mod n
● Biết m, An tìm lại M theo phương pháp đã thỏa thuận trước. Quá trình giải mã hoạt động vì ta có: cd ≡ med mod n
● Do ed≡1(mod p-1) và ed ≡1 (mod q-1) nên: med≡m (mod p) và med≡m (mod q).
● Do p và q là hai số nguyên tố cùng nhau, áp dụng định lý số dư Trung Quốc, ta có: med≡m (mod pq).