Chia sẻ source code chữ ký điện tử Elgamal bằng c#

Mô tả

Chữ ký số, chữ ký điện tử hay còn gọi là token được xem như con dấu điện tử, dùng để hỗ trợ doanh nghiệp trong các hoạt động như nộp thuế trực tuyến, giao dịch ngân hàng điện tử, kê khai hải quan điện tử, cổng thông tin quốc gia, kê khai bảo hiểm xã hội điện tử, ký hợp đồng với đối tác trực tuyến… mà không cần phải thực hiện các giấy tờ, thủ tục rườm rà như phương pháp truyền thống.

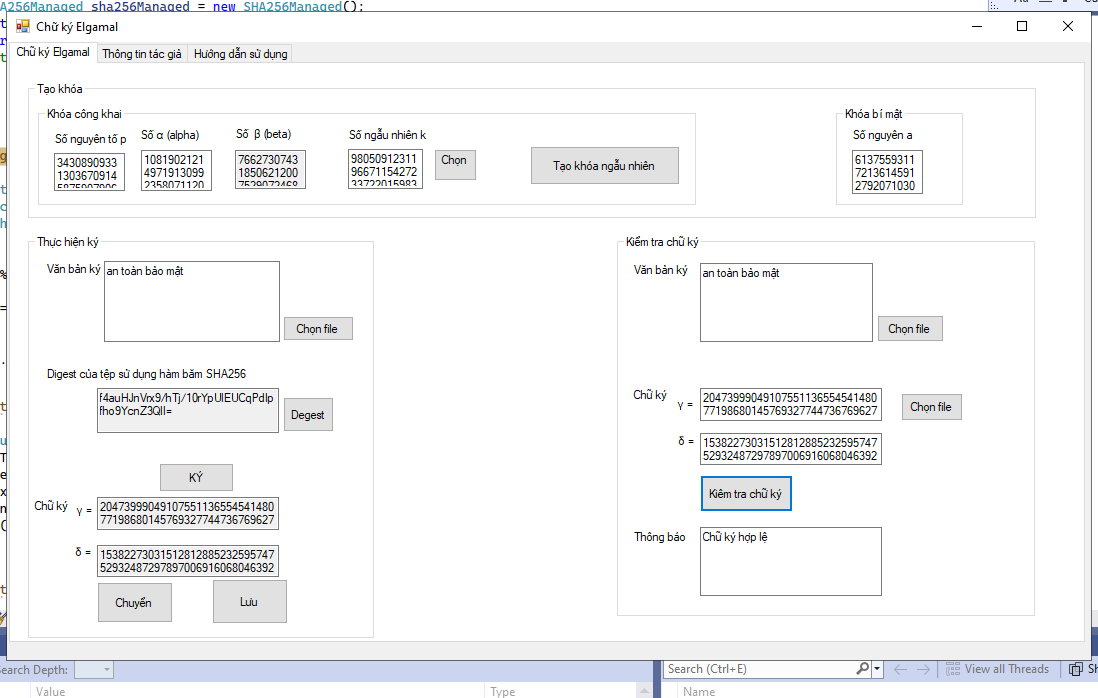
Sinh khóa
Việc sinh hệ mã hóa của ElGamal không khó như RSA. Chỉ đơn giản là chọn một số nguyên tố p, một hệ số alpha và một khóa bí mật a. Sau đó tính hệ số beta = alpha^a mod p. Đến đây bạn sẽ hỏi sao dễ thế, phần loằng ngoằng sẽ nói đến ở đoạn sau. Vậy ta có private key là a và p, public key là p, alpha, beta.
Ví dụ chọn luôn p = 11, alpha = 2, a = 3. Ta dễ dàng tính được beta = 2^3 = 8. Vậy ta có public key là p = 11, alpha = 2, beta = 8. Việc tính 8 là 2 mũ mấy (log2(8) = ?) thì dễ nhưng nếu 2 số này rất lớn và số p rất lớn thì việc thử toàn bộ các số mũ không ăn thua đâu.

Mã hóa
Giả sử với public key ở trên ta muốn mã hóa số x = 10, ta chọn một số k = 6 chẳng hạn. Ta tính 2 số:
y1 = alpha^k % p = 2^6 % 11 = 9 y2 = x*beta^k % p = 10 * 8^6 % 11 = 8
Ok giờ ta có bản mã cần gửi đi là e(y1, y2) = (9, 8). Số k thì bị bỏ đi, vụ này bàn sau.

Giải mã
Việc giải mã cũng dễ thôi, chỉ cần tính:
d(y1, y2) = y2 * (y1^-a) % p = 8 * (9^3)^-1 % 11 = 8 * 4 % 11 = 32 % 11 = 10 = x

Giải thích
Xem nào, ta sẽ thấy đc
x = y2 * (y1^-a) = x * beta^k * alpha^(-a*k) = x * alpha^(a*k) * alpha^(-a*k) = x
Dễ mà, đơn giản chỉ thế thôi 😎.